Maths Trignometric Ratios of Standard Angles Exercise18-2
Please Select
Q1 (i) cos 18°/sin 72°
(ii) tan 41°/cot 49°
(iii) cosec 17°30’/sec 72°30’
Solution :
 ,
,
Q2 (i) cot 40°/tan 50° – ½ (cos 35°/sin 55°)
(ii) (sin 49°/cos 41°)2 + (cos 41°/sin 49°)2
(iii) sin 72°/cos 18° – sec 32°/cosec 58°
(iv) cos 75°/sin 15° + sin 12°/cos 78°– cos 18°/sin 72°
(v) sin 25°/sec 65° + cos 25°/ cosec 65°.
Solution :
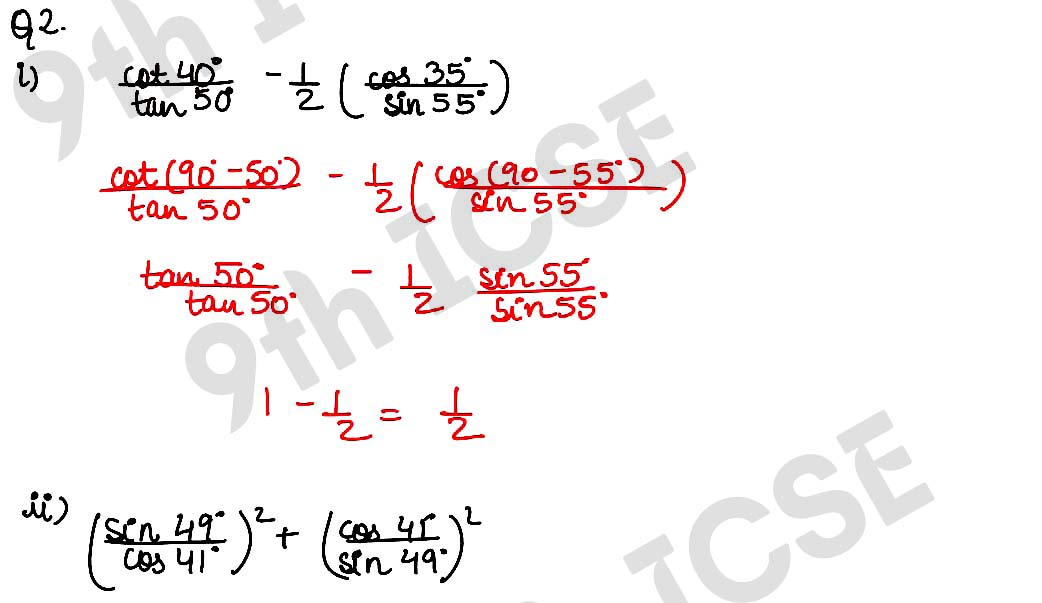 ,
, ,
, ,
,
Q3 (i) sin 62° – cos 28°
(ii) cosec 35° – sec 55°.
Solution :

Q4 (i) cos2 26° + cos 64° sin 26° + tan 36°/ cot 54°
(ii) sec 17°/cosec 73° + tan 68°/cot 22° + cos2 44° + cos2 46°.
Solution :
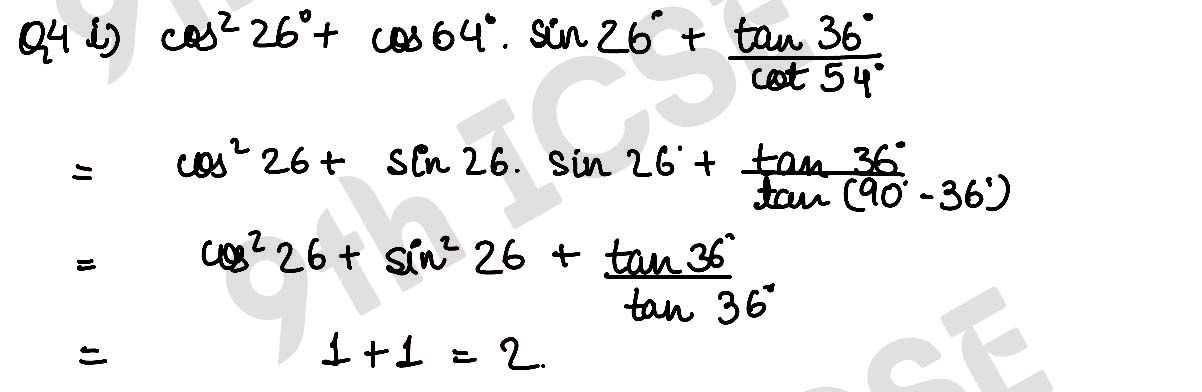 ,
,
Q5 (i) cos 65°/sin 25° + cos 32°/sin 58° – sin 28° sec 62° + cosec2 30°
(ii) sec 29°/ cosec 61° + 2 cot 8° cot 17° cot 45° cot 73° cot 82° – 3 (sin2 38° + sin2 52°).
Solution :
 ,
,
Q6 Express each of the following in terms of trigonometric ratios of angles between 0° to 45°:
(i) tan 81° + cos 72°
(ii) cot 49° + cosec 87°.
Solution :

Q7 (i) sin2 28° – cos2 62° = 0
(ii) cos2 25° + cos2 65° = 1
(iii) cosec2 67° – tan2 23° = 1
( iv) sec 222° – cot268° = 1.
Solution :
 ,
,
Q8 (i) sin 63° cos 27° + cos 63° sin 27° = 1
(ii) sec 31° sin 59° + cos 31° cosec 59° = 2.
Solution :
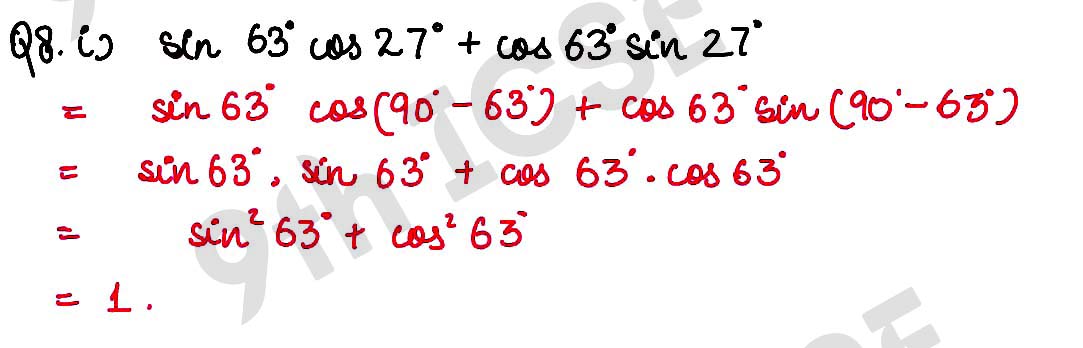 ,
,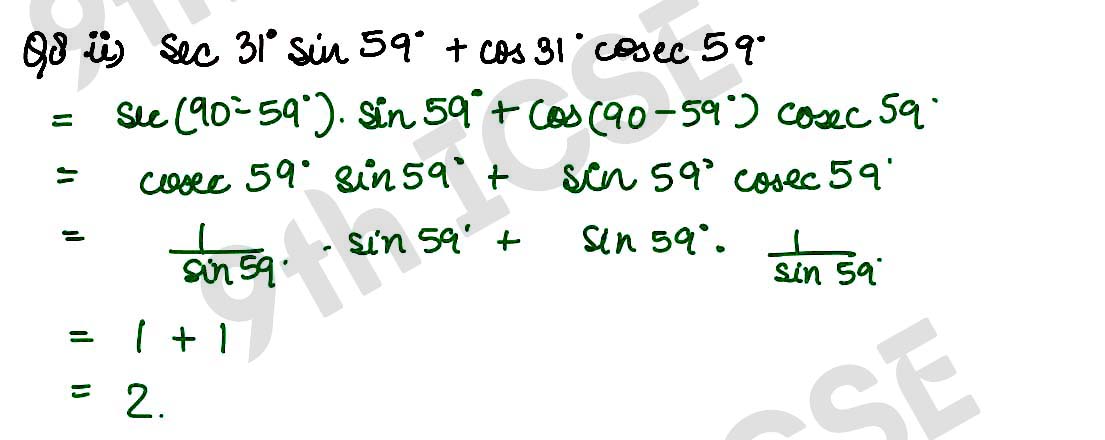
Q9 (i) sec 70° sin 20° – cos 20° cosec 70° = 0
(ii) sin2 20° + sin2 70° – tan2 45° = 0.
Solution :

Q10 (i) cot 54°/tan 36° + tan 20°/cot 70° – 2 = 0
(ii) sin 50°/cos 40° + cosec 40°/sec 50° – 4 cos 50° cosec 40° + 2 = 0.
Solution :
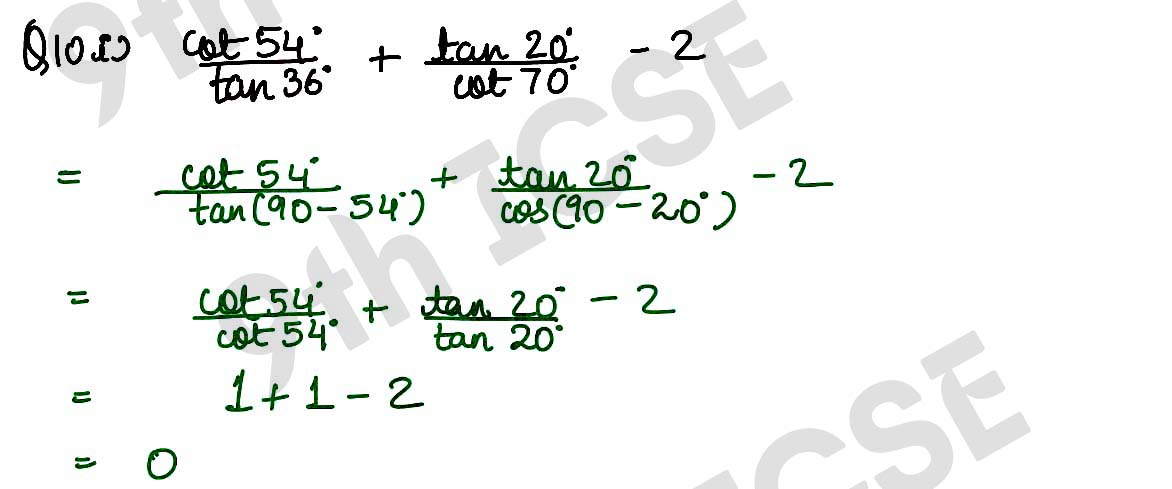 ,
,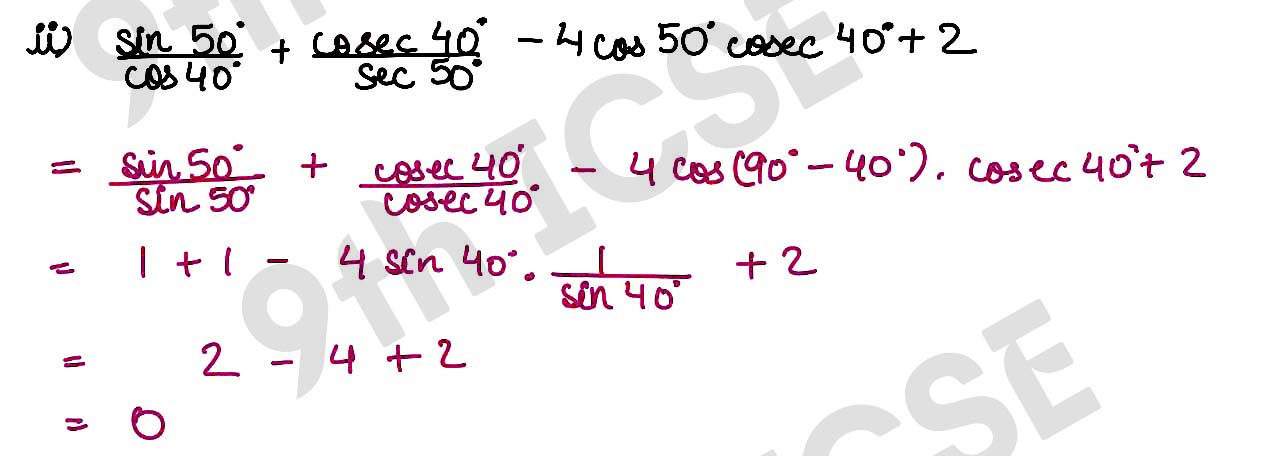
Q11 (i) cos 70° /sin 20° + cos 59°/sin 31° – 8 sin2 30° = 0 (ii) cos 80°/sin 10° + cos 59° cosec 31° = 2.
Solution :
 ,
,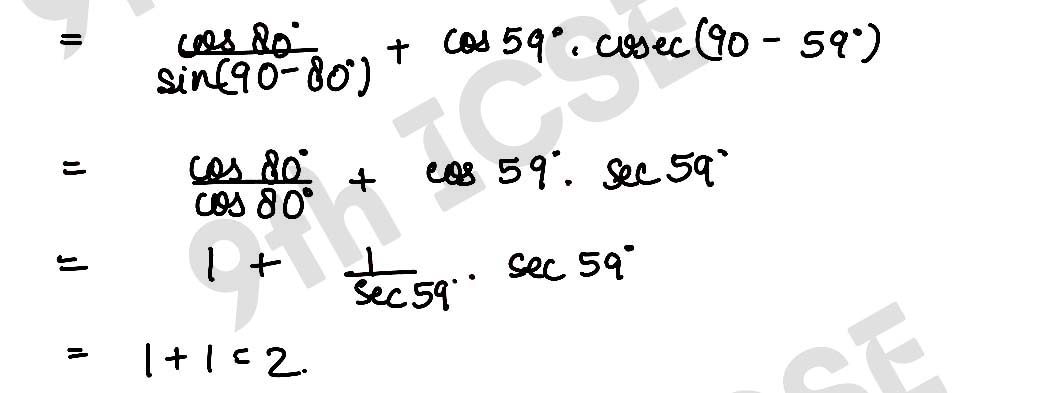
Q12 without using trigonometrical tables, evaluate:
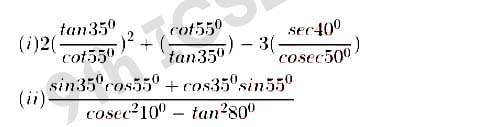
(iii) sin2 34° + sin2 56° + 2 tan 18° tan 72° – cot2 30°.
Solution :
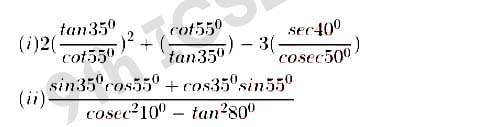 ,
,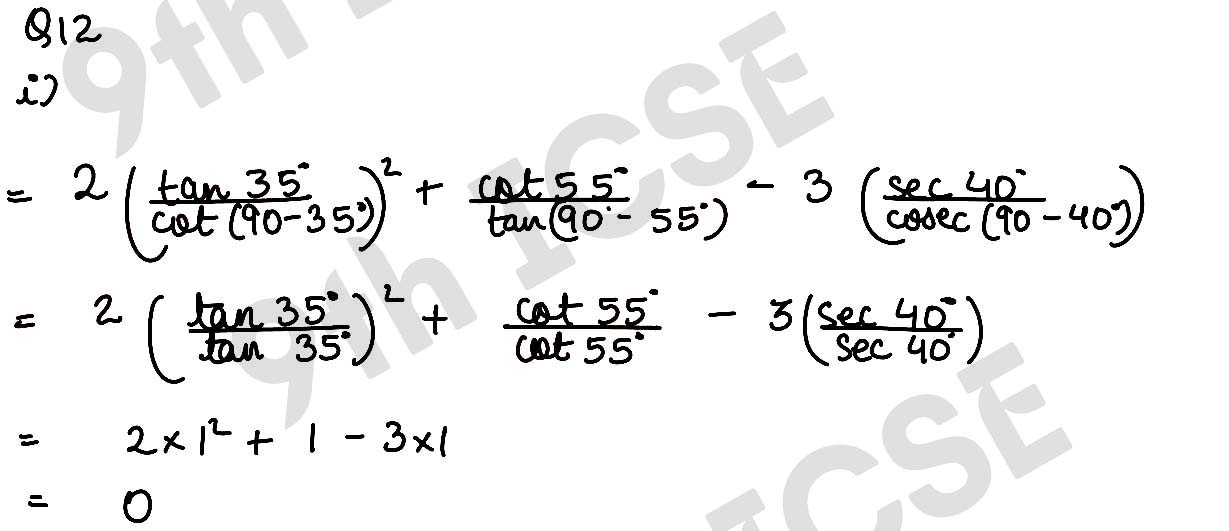 ,
, ,
,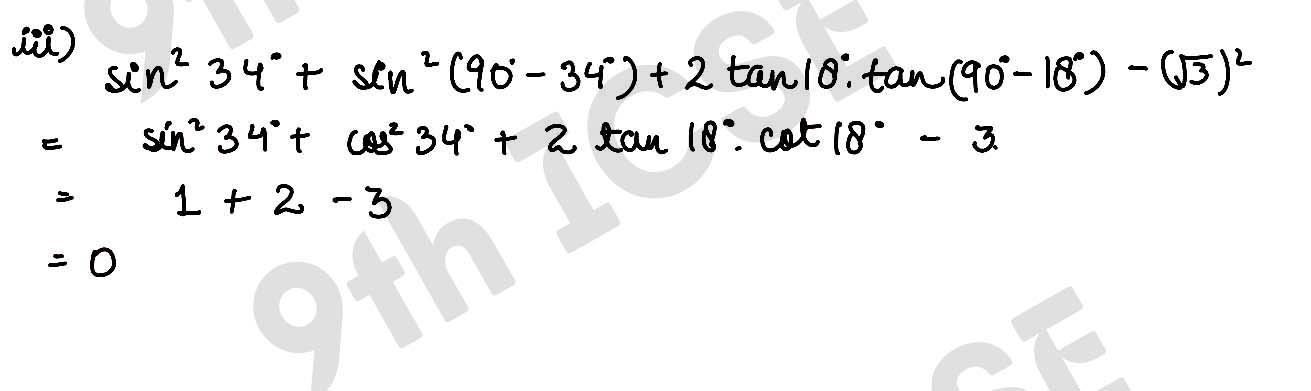
Q13 Prove the following:
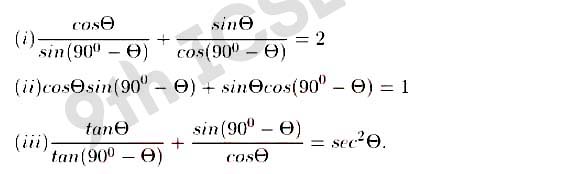
Solution :
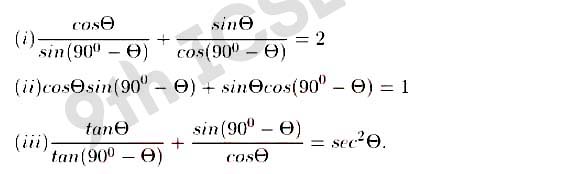 ,
,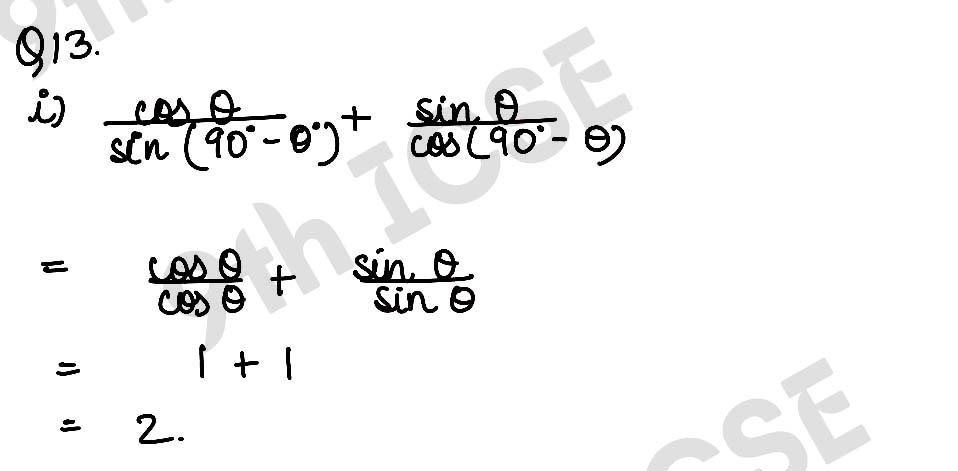 ,
,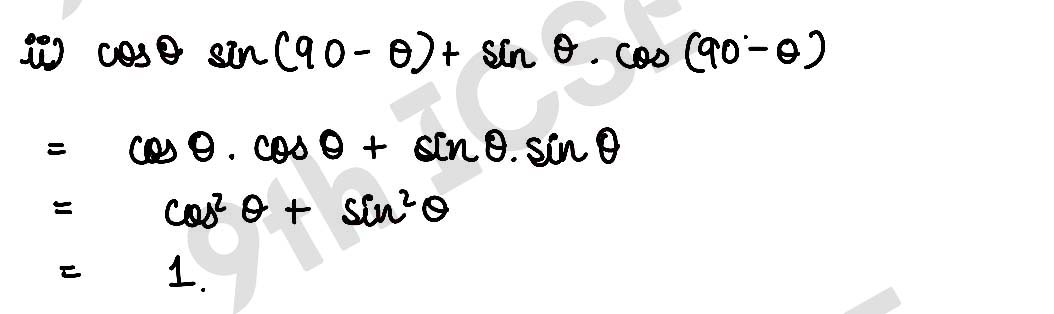 ,
,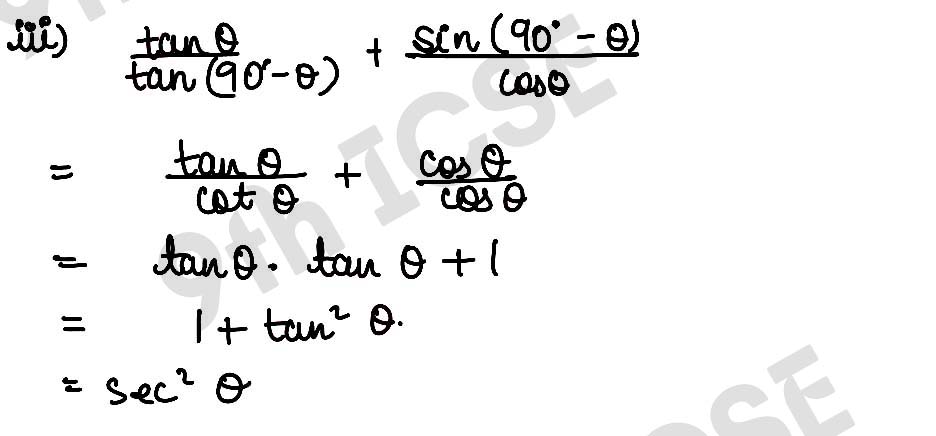
Q14 Prove the following
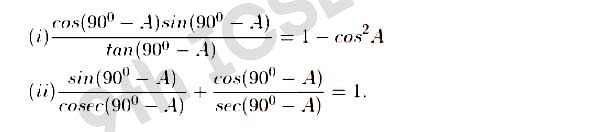
Solution :
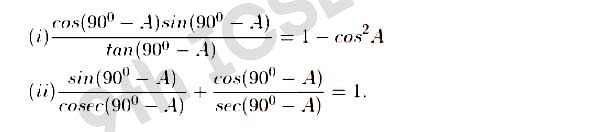 ,
,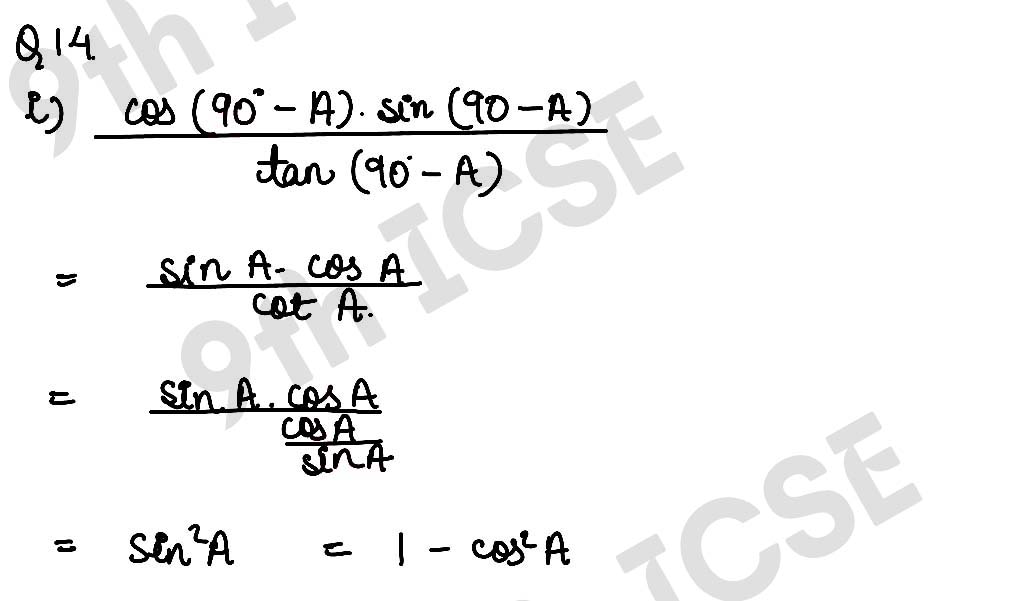 ,
,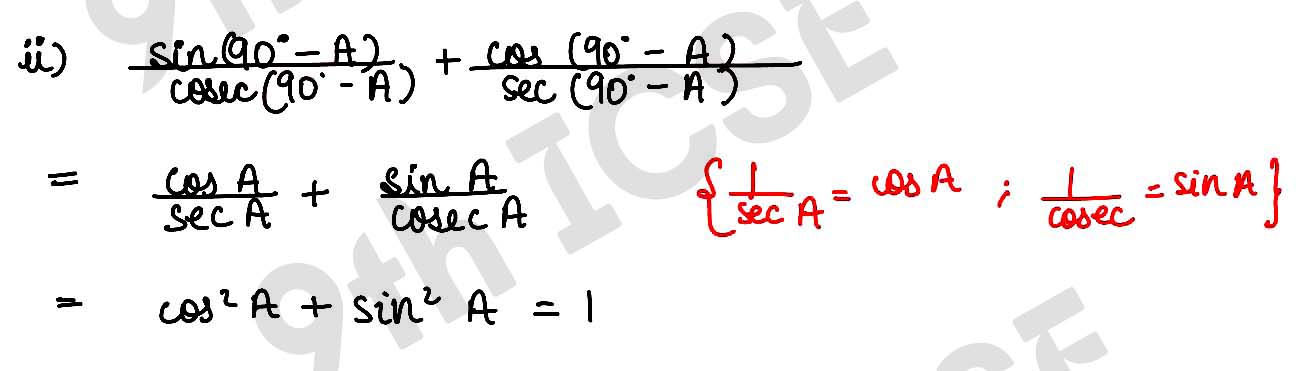
Q15 Simply the following
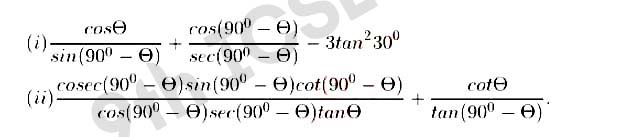
Solution :
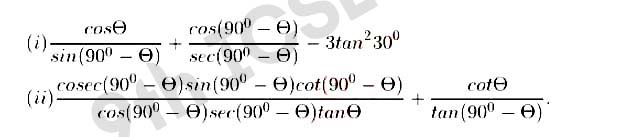 ,
,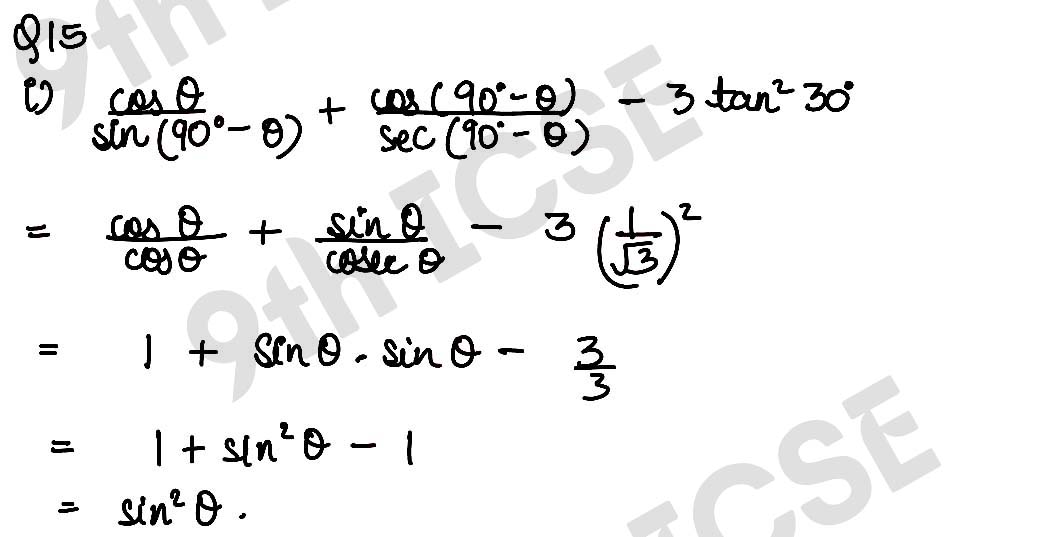 ,
,
Q16 Show that:
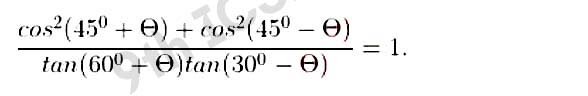
Solution :
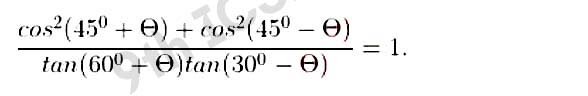 ,
,
Q17 Find the value of A if
(i) sin 3A = cos (A – 6°), where 3A and A – 6° are acute angles
(ii) tan 2A = cot (A – 18°), where 2A and A – 18° are acute angles
(iii) If sec 2A = cosec (A – 27°) where 2A is an acute angle, find the measure of ∠A.
Solution :
 ,
, ,
,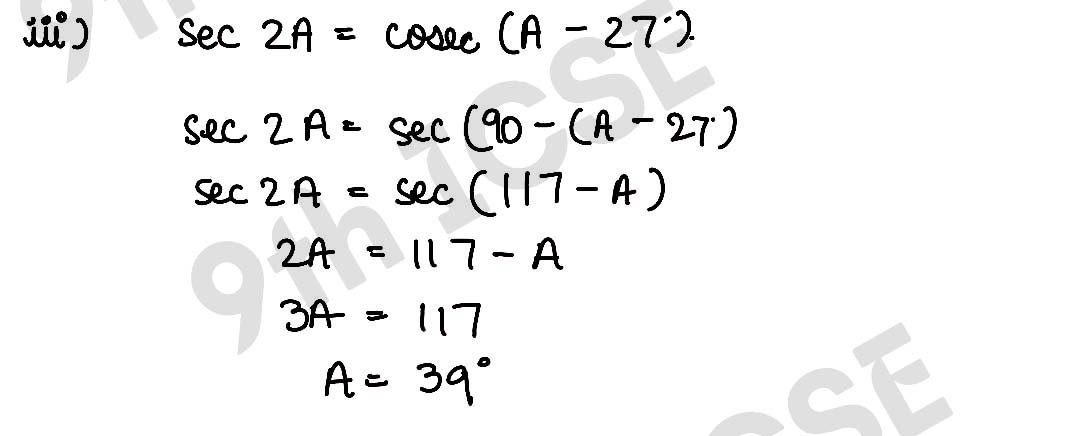
Q18 Find the value of θ (0° < θ < 90°) if:
(i) cos 63° sec (90° – θ)=1
(ii) tan 35° cot (90° – θ)=1.
Solution :
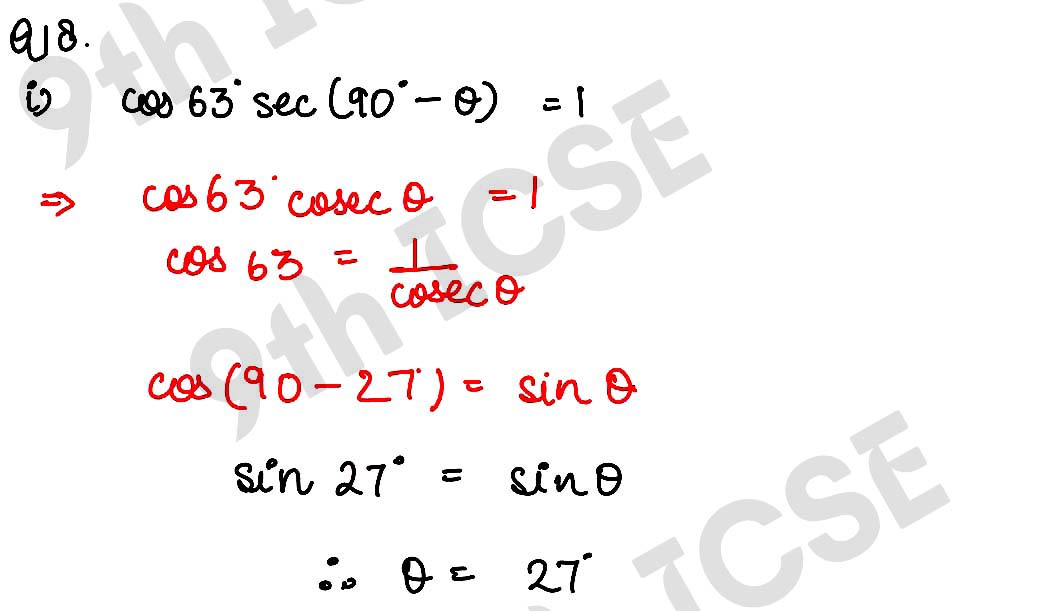 ,
,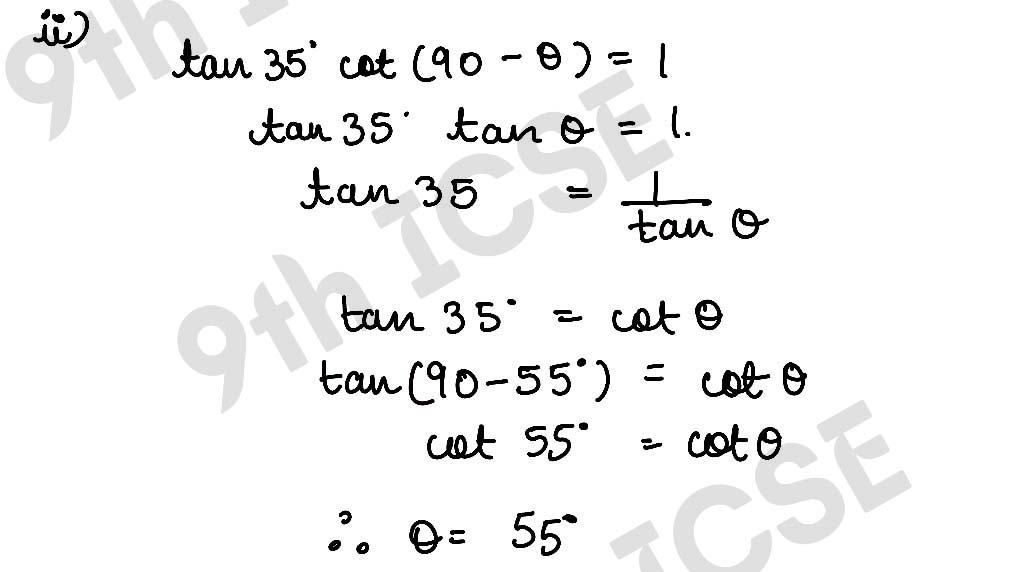
Q19 If A, B and C are the interior angles of a △ ABC, show that
(i) cos (A + B)/2 = sin C/2
(ii) tan (C + A)/2 = cot B/2.
Solution :
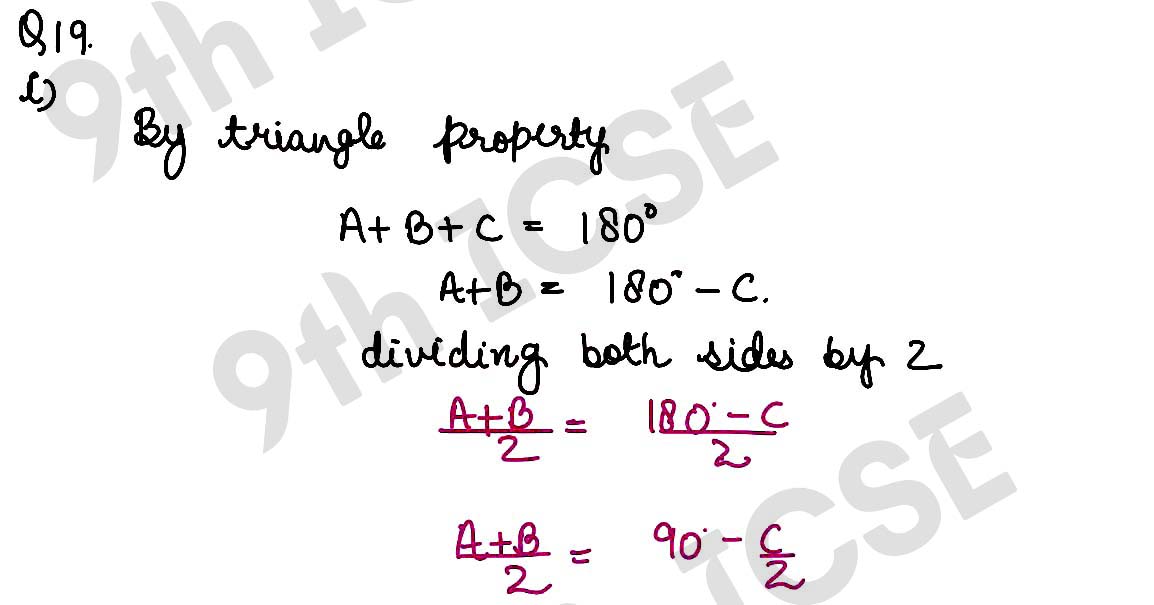 ,
, ,
,
Contact Us
