Maths Trignometric Ratios of Standard Angles Exercise18-1
Please Select
Q1 Find the values of
(i) 7 sin 30° cos 60°
(ii) 3 sin2 45° + 2 cos2 60°
(iii) cos2 45° + sin2 60° + sin2 30°
(iv) cos 90° + cos2 45° sin 30° tan 45°.
Solution :
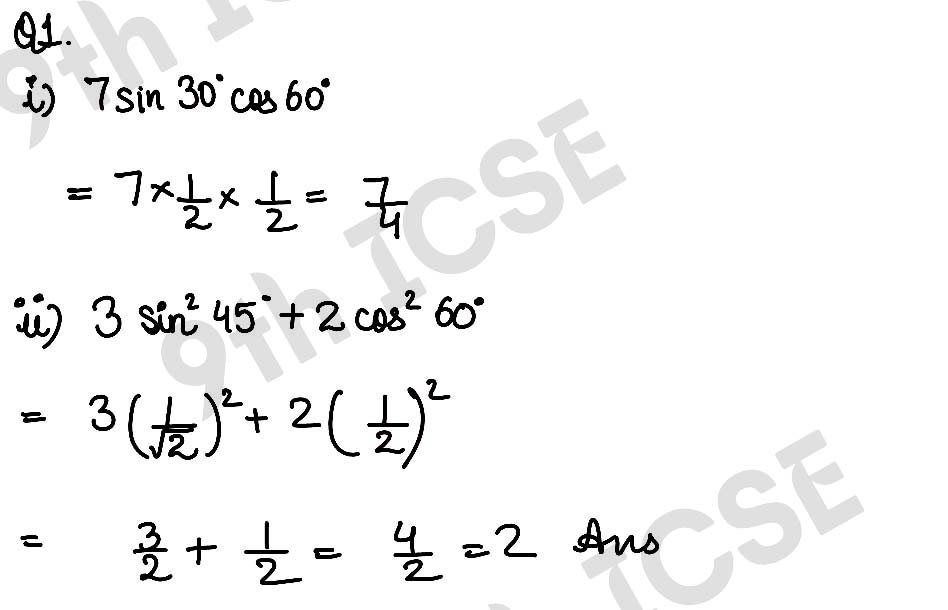 ,
,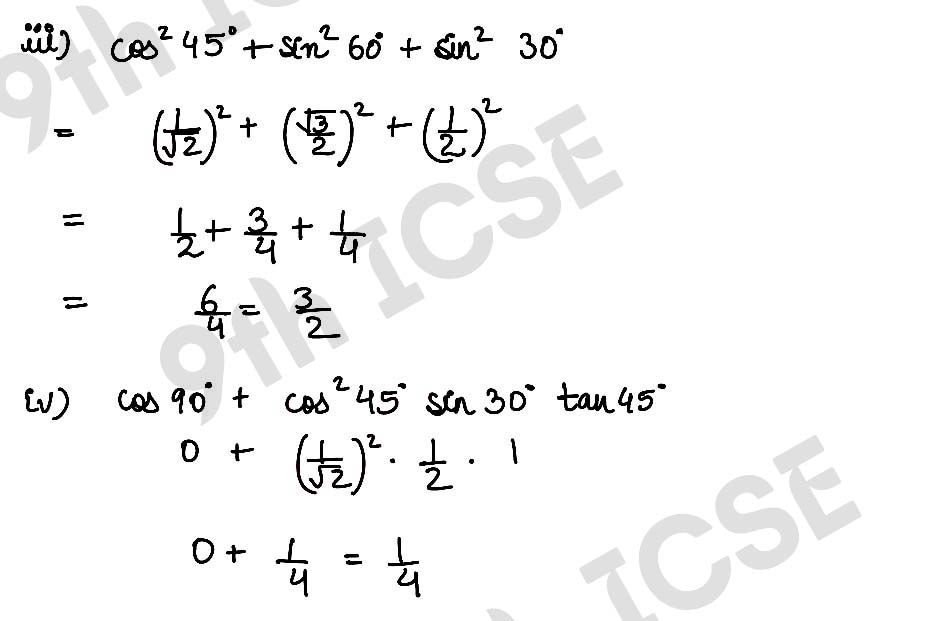
Q2 Find the values of (i) (sin245° + cos245°)/tan260° (ii) (sin30° – sin90° + 2cos0°)/tan2 60° (iii) 4/3 tan230° + sin260° – 3cos260° + 3/4 tan260° – 2tan245°
Solution :
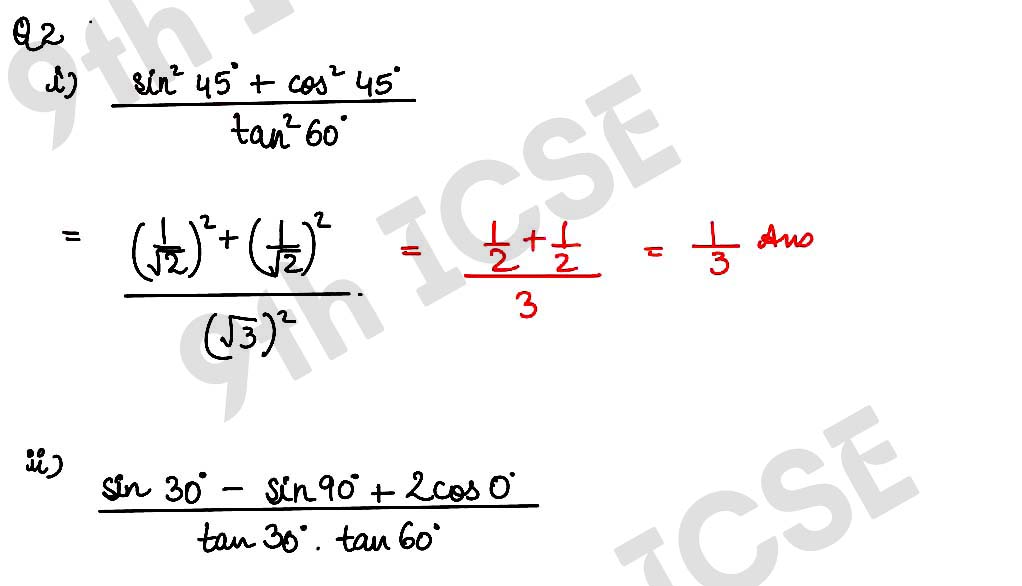 ,
, ,
,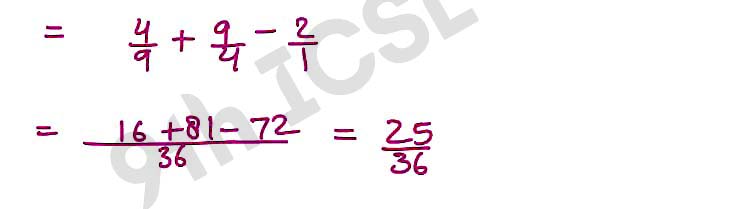
Q3 Find the values of
(i) (sin30°/cos245°) – 3tan30° + 5cos90°
(ii) 2√2 cos45° cos60° + 2√3 sin30° tan60° – cos30°
(iii) 4/5 tan260° – (2/sin230°) – 3/4 tan230°
Solution :
 ,
,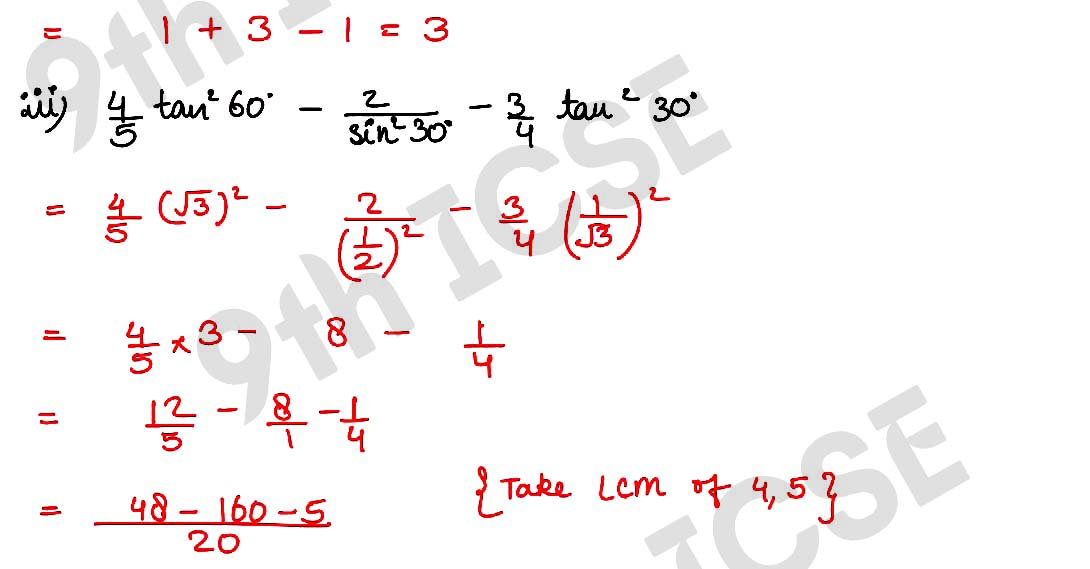 ,
,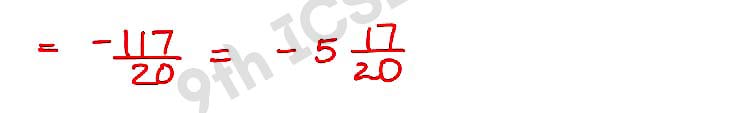
Q4 Prove That.
(i) cos2 30° + sin 30° + tan2 45° = 2 ¼
(ii) 4 (sin4 30° + cos4 60°) – 3 (cos2 45° – sin2 90°) = 2
(iii) cos 60° = cos2 30° – sin2 30°.
Solution :
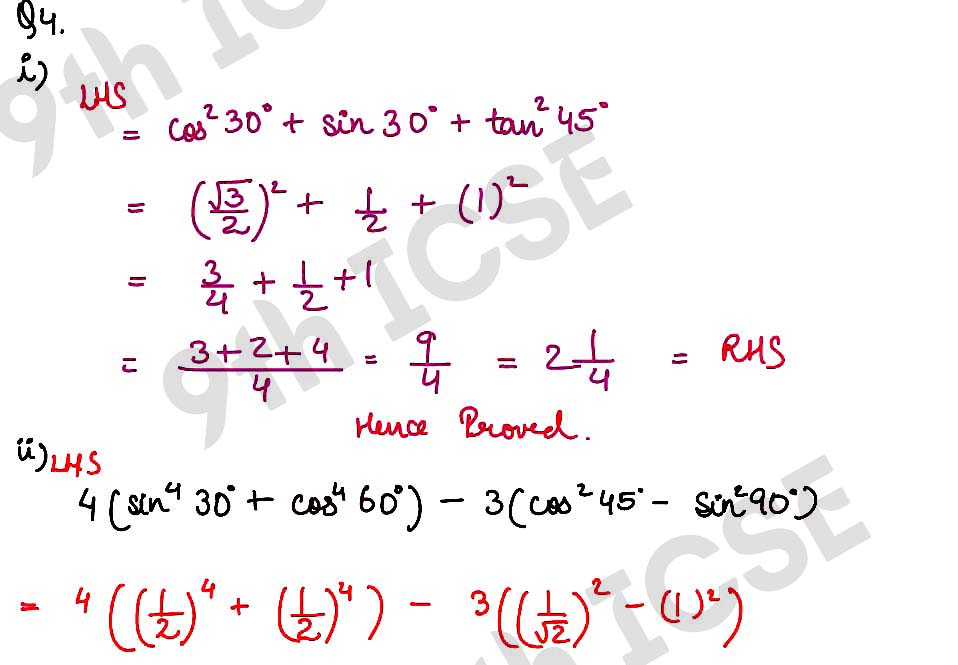 ,
, ,
,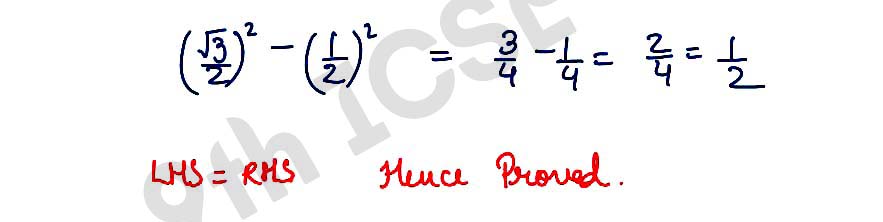
Q5 (i) If x = 300, verify that tan 2x = 2tanx/ (1- tan2 x).
(ii) If x = 150, verify that 4 sin 2x cos 4x sin 6x = 1.
Solution :
 ,
,
Q6 Find the values of
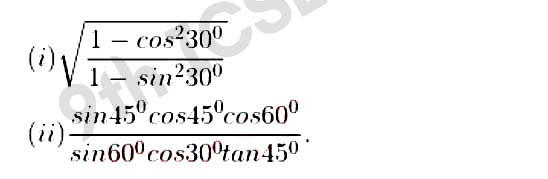
Solution :
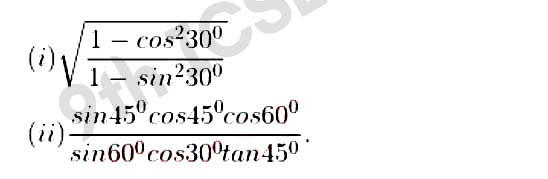 ,
,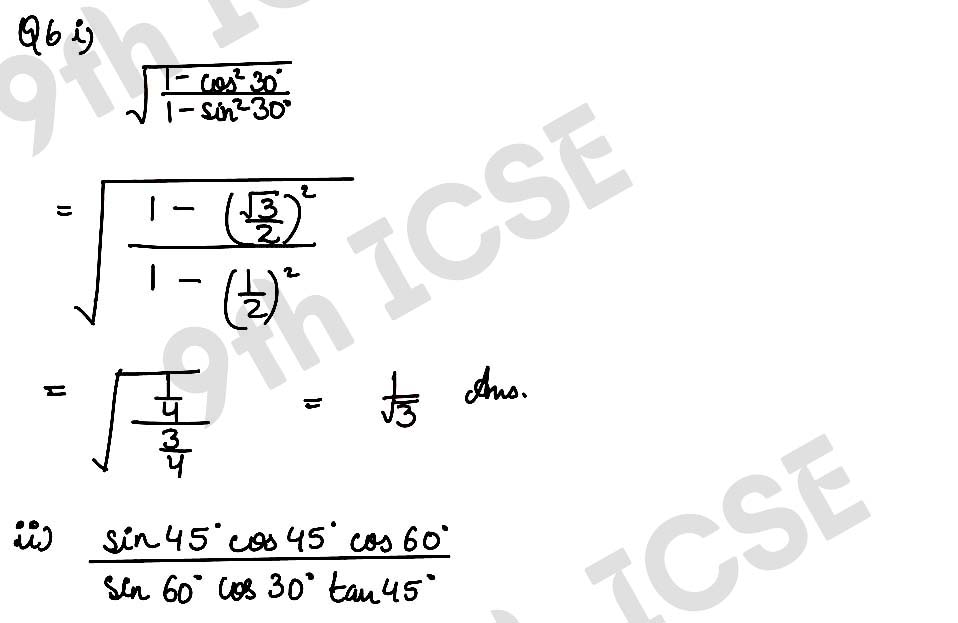 ,
,
Q7 If θ = 30°, verify that
(i) sin 2θ = 2 sin θ cos θ
(ii) cos 2θ = 2 cos2 θ – 1
(iii) sin 3θ = 3 sin θ – 4 sin3 θ
(iv) cos 3θ = 4 cos3 θ – 3 cos θ.
Solution :
 ,
, ,
, ,
,
Q8 If θ = 30°, find the ratio 2 sin θ: sin 2 θ.
Solution :

Q9 By means of an example, show that sin (A + B) ≠ sin A + sin B.
Solution :

Q10 If A = 60° and B = 30°, verify that
(i) sin (A + B) = sin A cos B + cos A sin B
(ii) cos (A + B) = cos A cos B – sin A sin B
(iii) sin (A – B) = sin A cos B – cos A sin B
(iv) tan (A – B) = (tan A – tan B)/ (1 + tan A tan B).
Solution :
 ,
, ,
, ,
, ,
,
Q11 (i) If 2θ is an acute angle and 2 sin 2θ = √3, find the value of θ.
(ii) If 20° + x is an acute angle and cos (20° + x) = sin 60°, then find the value of x.
(iii) If 3 sin2 θ = 2 ¼ and θ is less than 90°, find the value of θ.
Solution :
 ,
,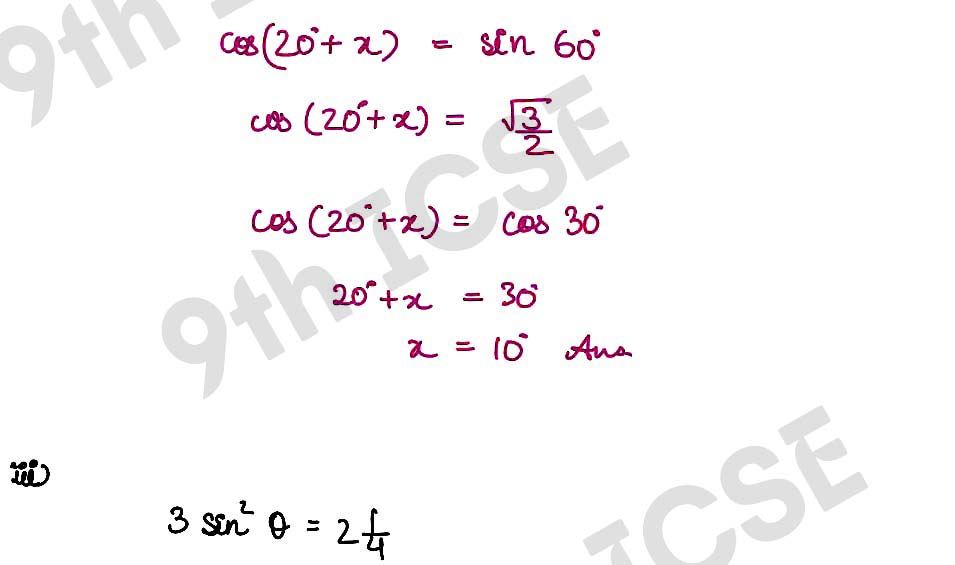 ,
,
Q12 If θ is an acute angle and sin θ = cos θ, find the value of θ and hence, find the value of 2 tan2 θ + sin2 θ – 1.
Solution :
 ,
,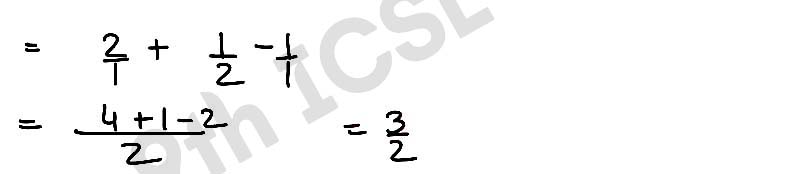
Q13 From the adjoining figure, find
(i) tan x°
(ii) x
(iii) cos x°
(iv) use sin x° to find y.
Solution :
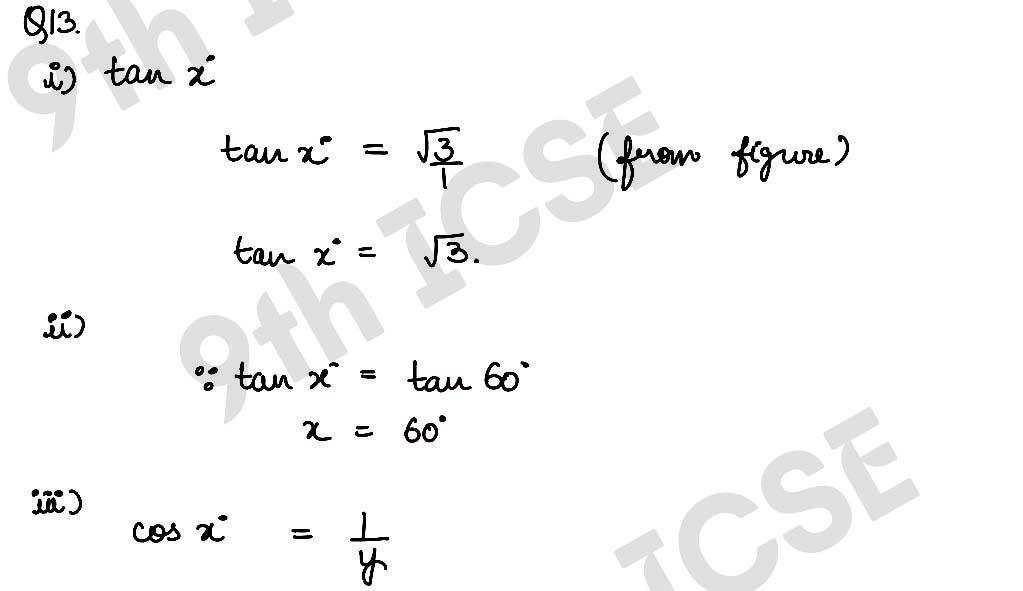 ,
, ,
,
Q14 If 3θ is an acute angle, solve the following equations for θ:
(i) 2 sin 3θ = √3
(ii) tan 3θ = 1.
Solution :
 ,
,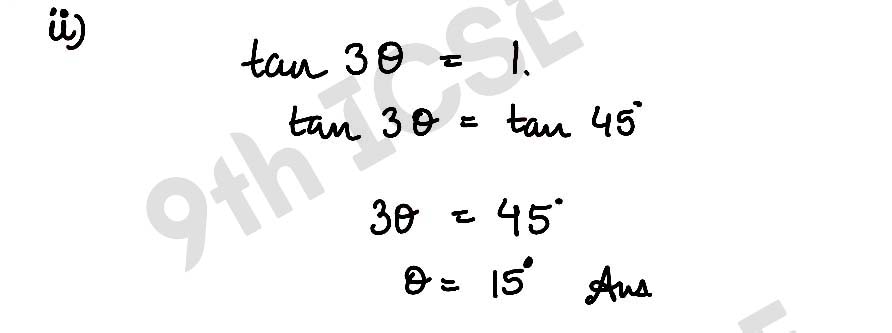
Q15 If tan 3x = sin 45° cos 45° + sin 30°, find the value of x.
Solution :
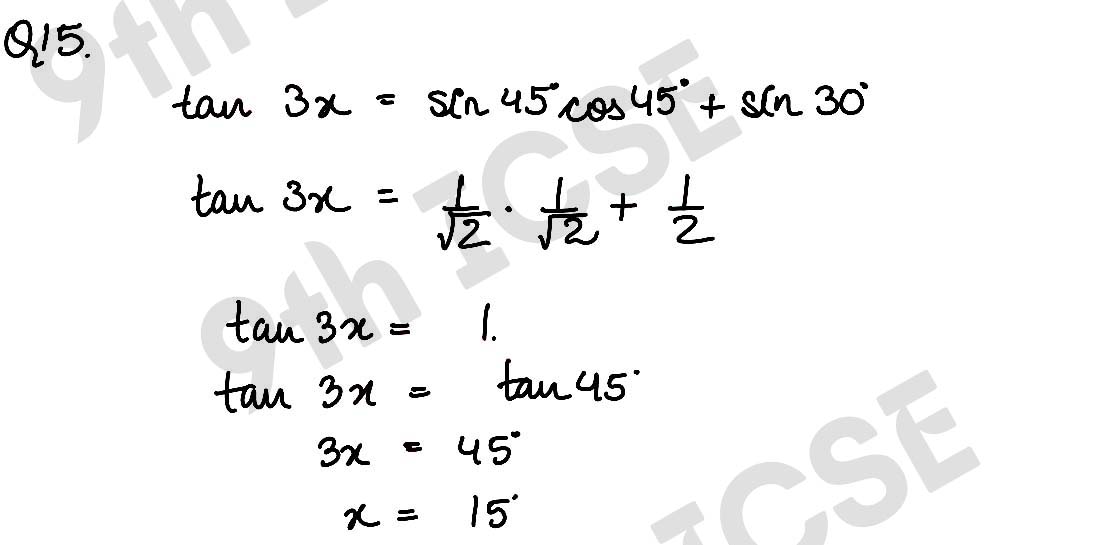
Q16 If 4 cos2 x° – 1 = 0 and 0 ≤ x ≤ 90, find
(i) x
(ii) sin2 x° + cos2 x°
(iii) cos2 x° – sin2 x°
Solution :
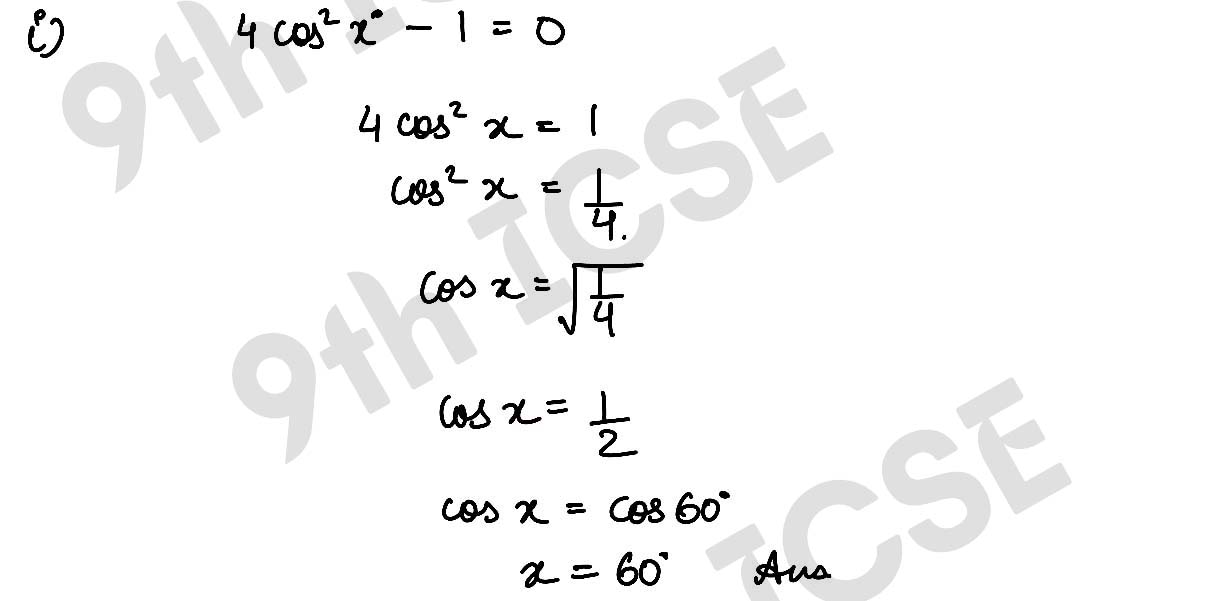 ,
,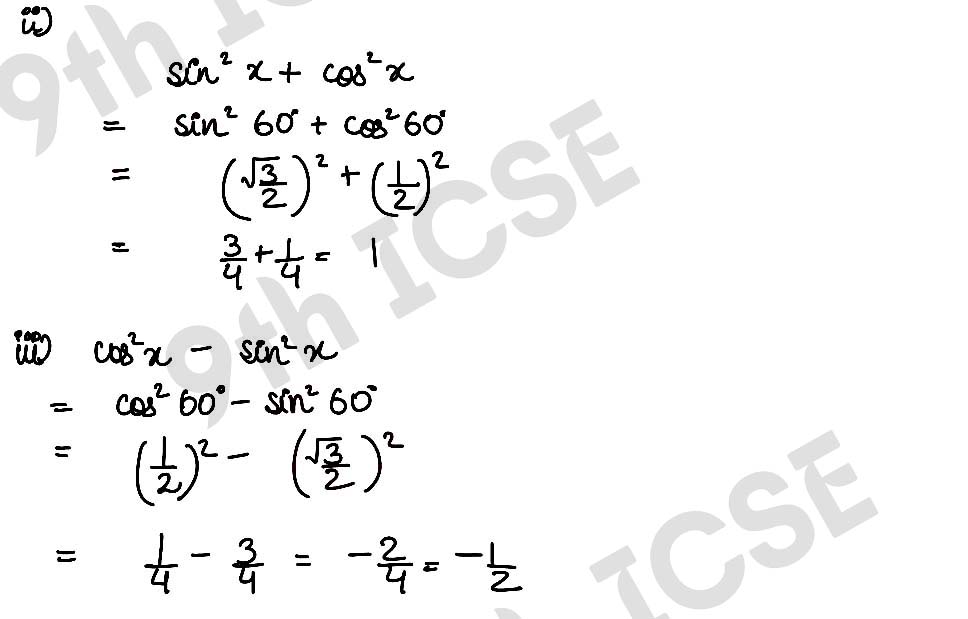
Q17 (i) If sec θ = cosec θ and 0° ≤ θ ≤ 90°, find the value of θ.
(ii) If tan θ = cot θ and 0° ≤ θ ≤ 90°, find the value of θ
Solution :
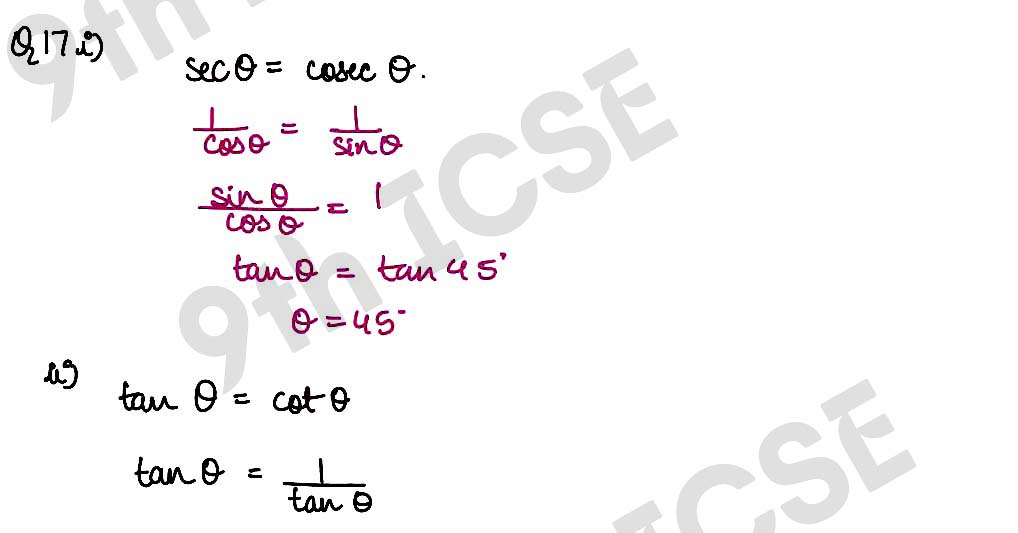 ,
,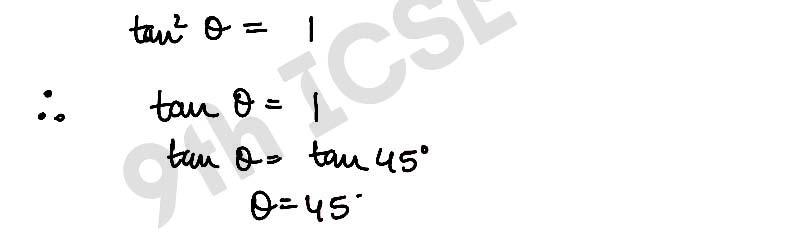
Q18 If sin 3x = 1 and 0° ≤ 3x ≤ 90°, find the values of
(i) sin x
(ii) cos 2x
(iii) tan2 x – sec2 x.
Solution :
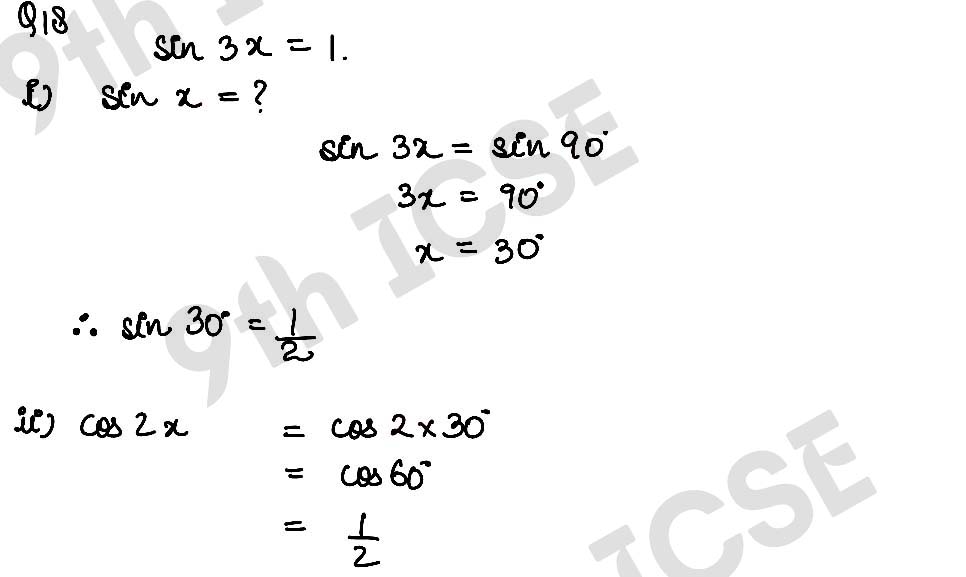 ,
,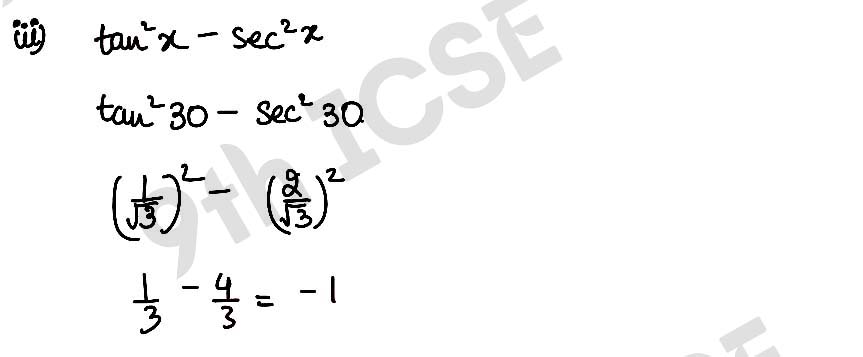
Q19 If 3 tan2 θ – 1 = 0, find cos 2θ, given that θ is acute.
Solution :
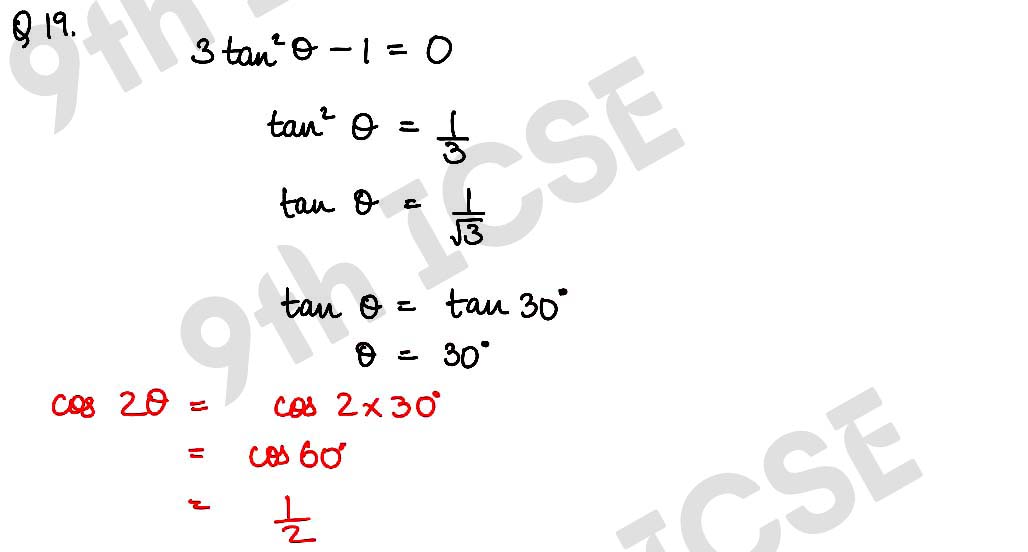
Q20 If sin x + cos y = 1, x = 30° and y is acute angle, find the value of y.
Solution :
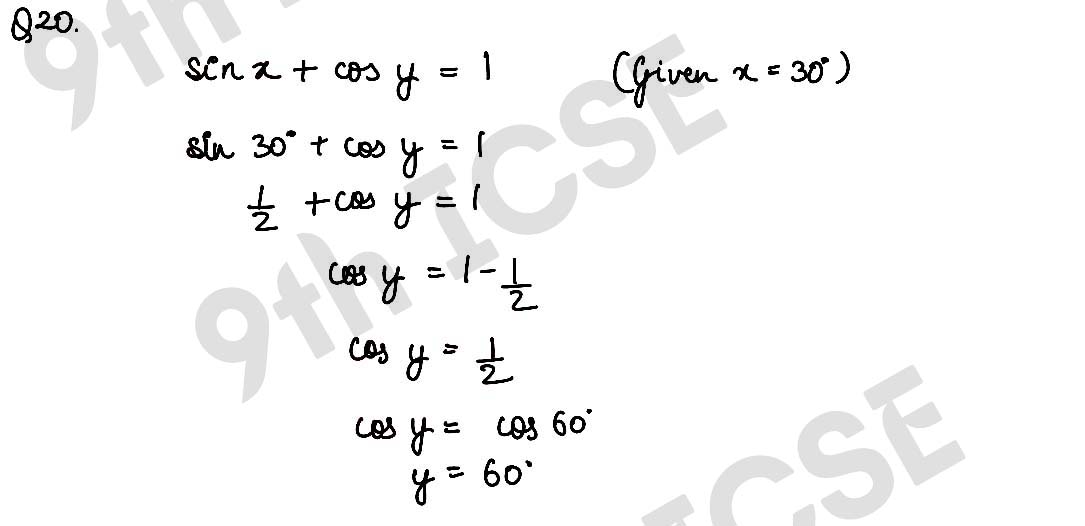
Q21 If sin (A + B) = √3/2 = cos (A – B), 0° < A + B ≤ 90° (A> B), find the values of A and B.
Solution :
 ,
,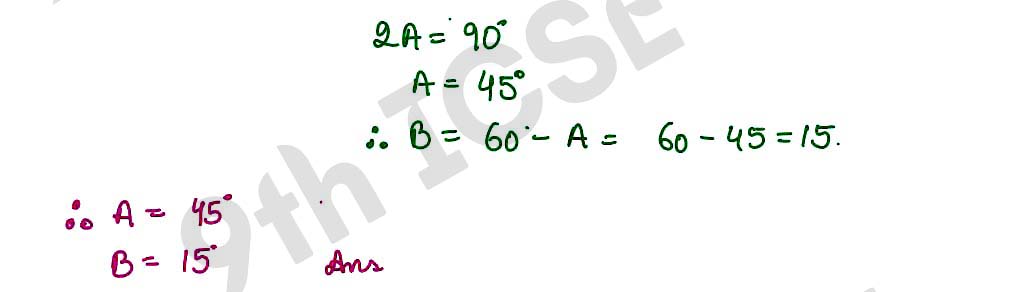
Q22 If the length of each side of a rhombus is 8 cm and its one angle is 60°, then find the lengths of the diagonals of the rhombus.
Solution :
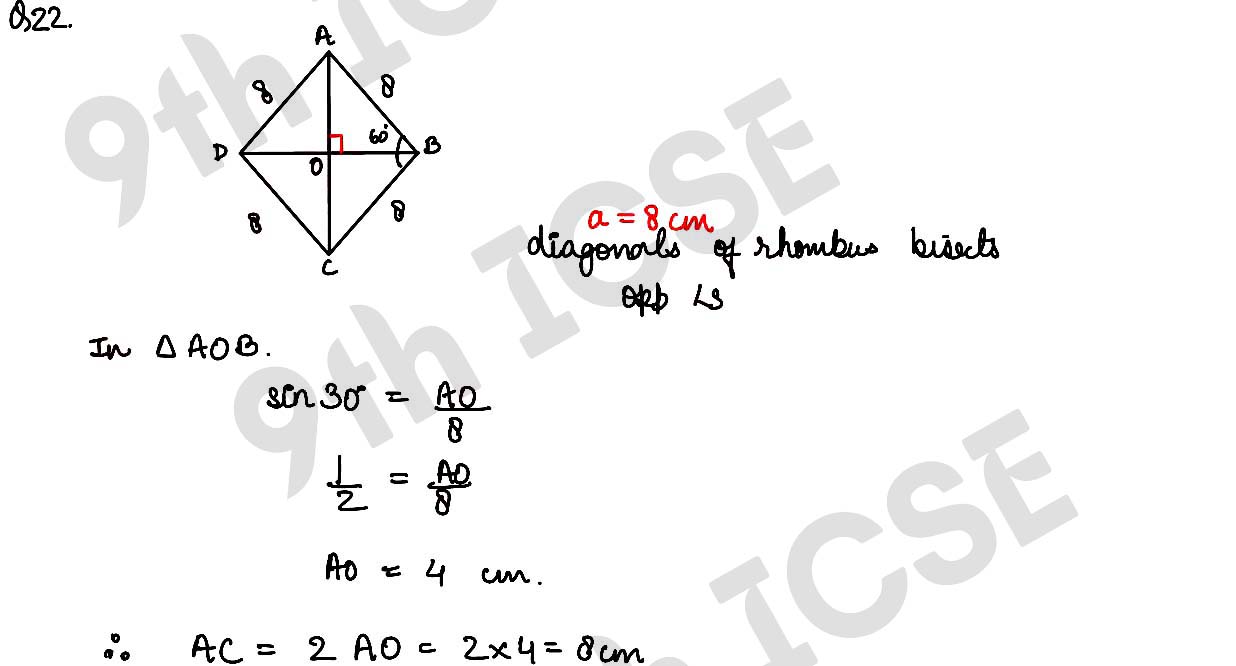 ,
,
Q23 In the right-angled triangle ABC, ∠C = 90° and ∠B = 60°. If AC = 6 cm, find the lengths of the sides BC and AB.
Solution :
 ,
,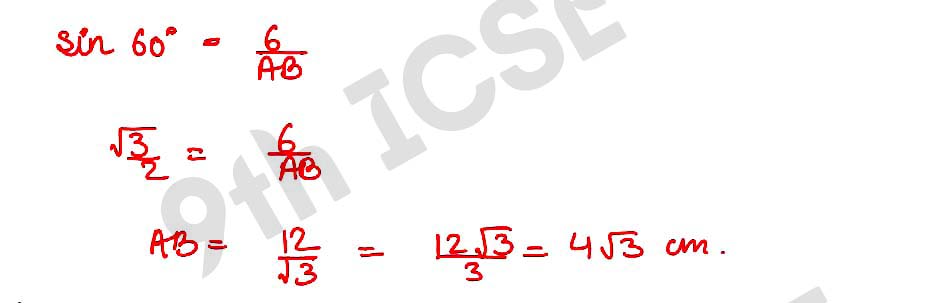
Q24 In the adjoining figure, AP is a man of height 1.8 m and BQ is a building 13.8 m high. If the man sees the top of the building by focusing his binoculars at an angle of 30° to the horizontal, find the distance of the man from the building.
Solution :

Q25 In the adjoining figure, ABC is a triangle in which ∠B = 45° and ∠C = 60°. If AD ⟂ BC and BC = 8 m, find the length of the altitude AD.
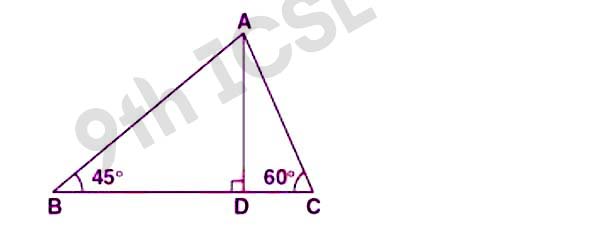
Solution :
 ,
, ,
, ,
,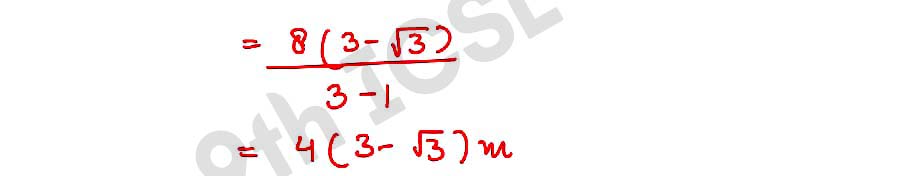
Contact Us
