Maths Trignometric Ratios of Standard Angles Chaptertest
Please Select
Q1 (i) sin2 60° – cos2 45° + 3tan2 30°
(ii)
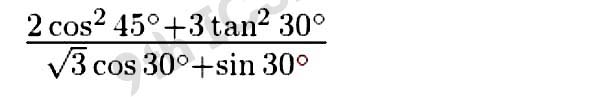
(iii) sec 30° tan 60° + sin 45° cosec 45° + cos 30° cot 60°
Solution :
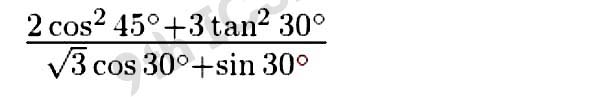 ,
, ,
,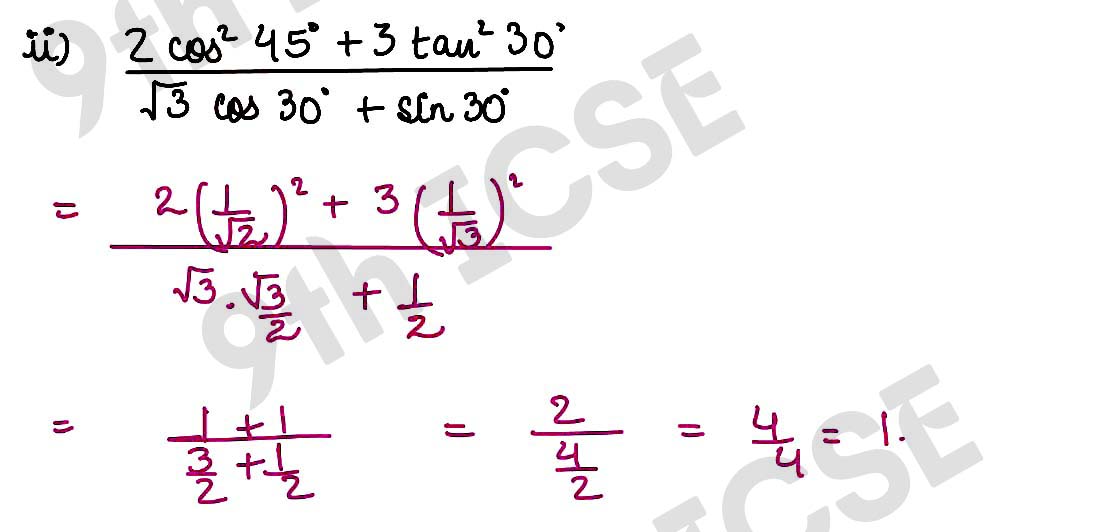 ,
,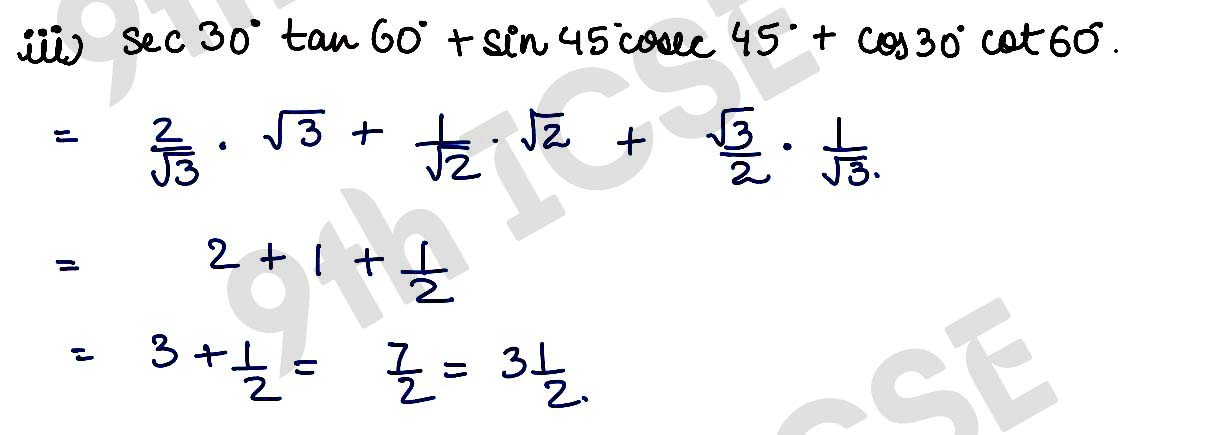
Q2 Taking A = 30°, verify that
(i) cos4 A – sin4 A = cos 2A
(ii) 4cos A cos (60° – A) cos (60° + A) = cos 3 A.
Solution :
 ,
,
Q3 If A = 45° and B = 30°, verify that sin A/ (cos A + sin A + sin B) = 2/3
Solution :

Q4 Taking A = 60° and B = 30°, verify that
(i) sin (A + B)/ cos A cos B = tan A + tan B
(ii) sin (A – B)/ sin A sin B = cot B – cot A
Solution :
 ,
,
Q5 If √2 tan 2θ = √6 and θ° < 2θ < 90°, find the value of sin θ + √3 cos θ – 2 tan2 θ.
Solution :
 ,
,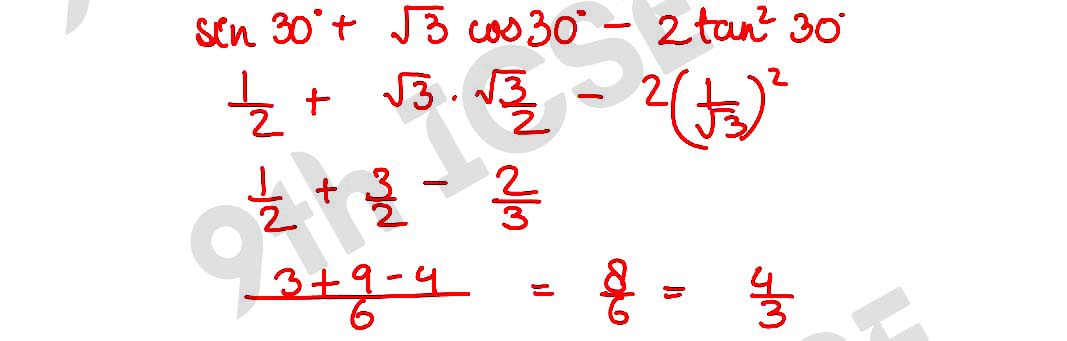
Q6 If 3θ is an acute angle, solve the following equations for θ:
(i) (cosec 3θ – 2) (cot 2θ – 1) = 0
(ii) (tan θ – 1) (cosec 3θ – 1) = 0
Solution :
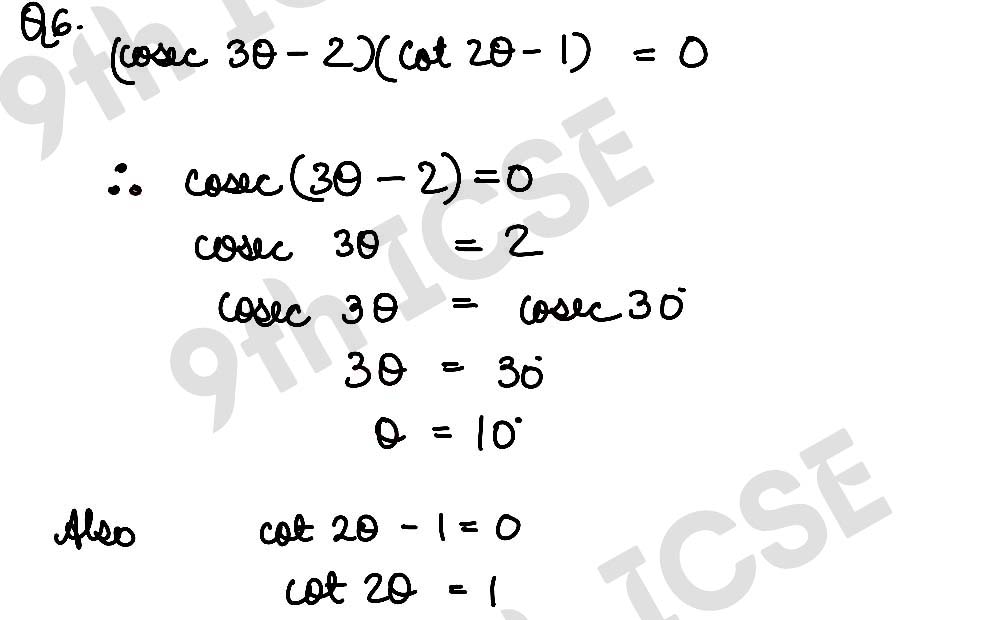 ,
,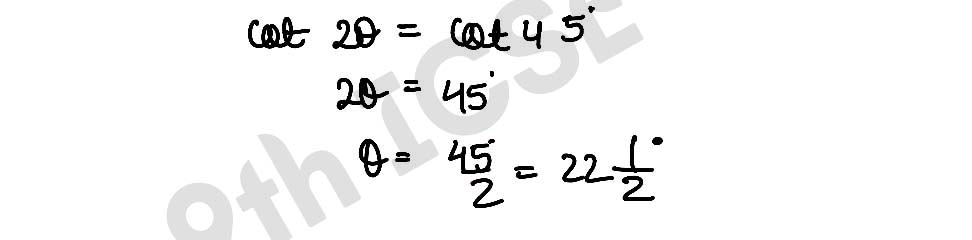
Q7 If tan (A + B) = √3 and tan (A – B) = 1 and A, B (B < A) are acute angles, find the values of A and B.
Solution :

Q8 Without using trigonometrical tables, evaluate the following:
(i) sin2 28° + sin2 62° – tan2 45°
(ii) 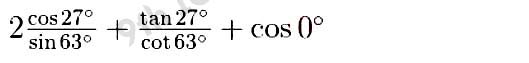
(iii) cos 18° sin 72° + sin 18° cos 72°
(iv) 5 sin 50° sec 40° – 3 cos 59° cosec 31°
Solution :
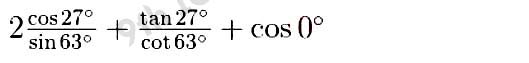 ,
,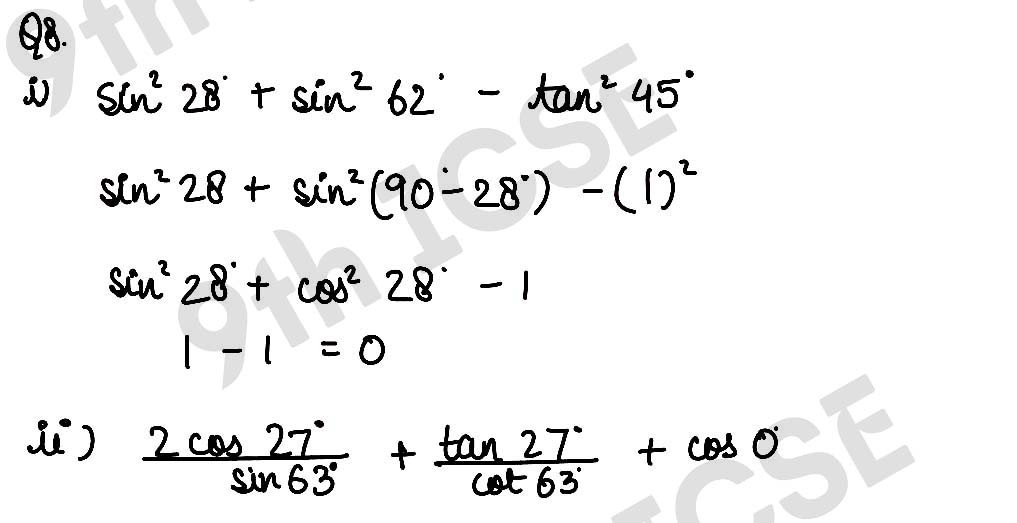 ,
,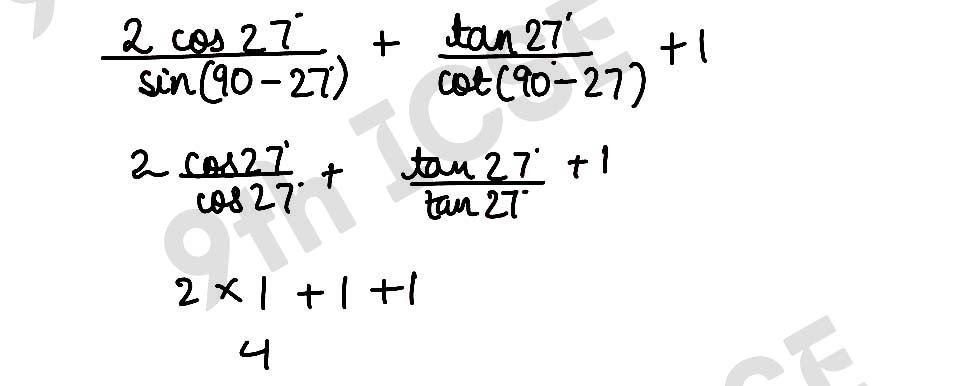 ,
,
Q9 Prove that:
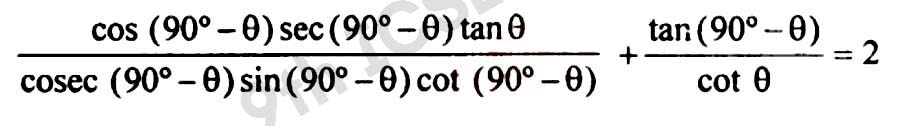
Solution :
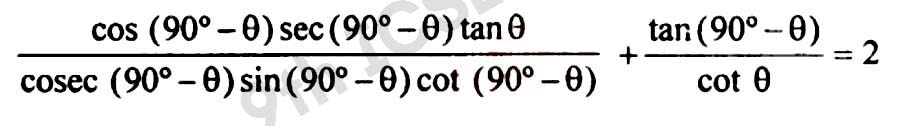 ,
,
Q10 When 0° < A < 90°, solve the following equations:
(i) sin 3A=cos 2A
(ii) tan 5A=cot A
Solution :
 ,
,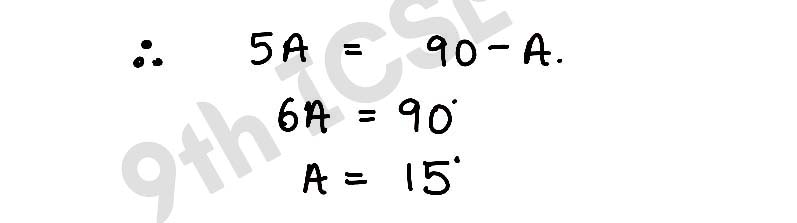
Q11 Find the value of θ if
(i) sin (θ + 36°) = cos θ, where θ and θ + 36° are acute angles.
(ii) sec 4θ = cosec (θ – 20°), where 4θ and θ – 20° are acute angles.
Solution :
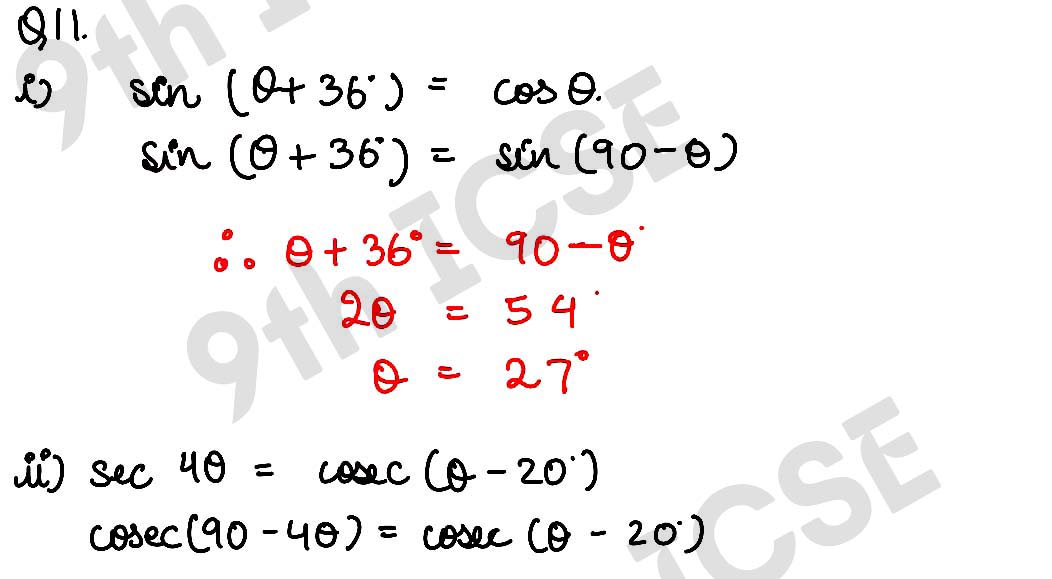 ,
,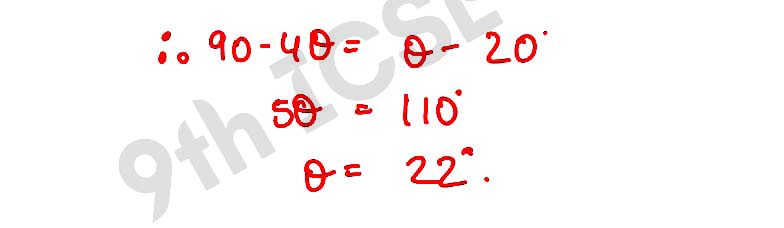
Q12 In the adjoining figure, ABC is right-angled triangle at B and ABD is right angled triangle at A. If BD ⊥ AC and BC = 2√3cm, find the length of AD.
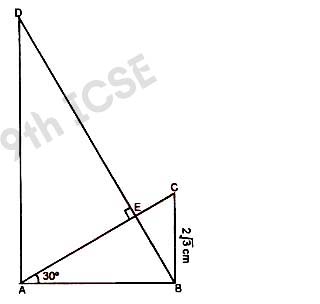
Solution :
 ,
, ,
,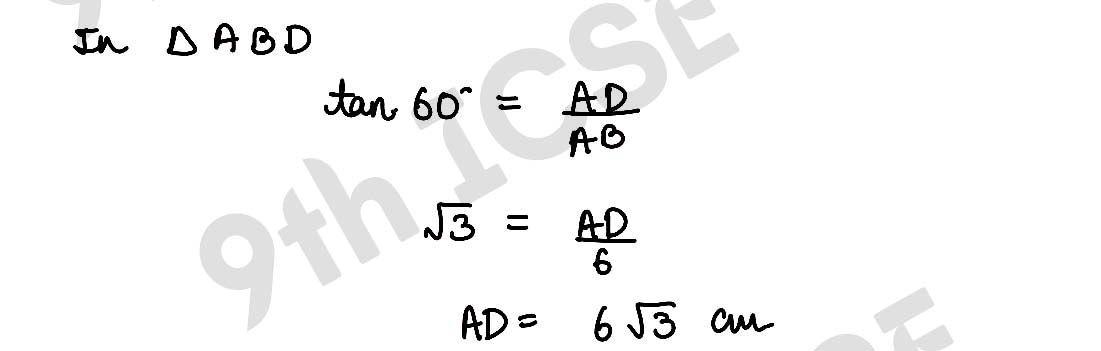
Contact Us
