Maths Rational and irrational Numbers Chaptertest
Please Select
Q1 Without act/JPEGual division, find whether the following rational numbers are terminating decimals or recurring decimals:
(i) 13/45
(ii) -5/56
(iii) 7/125
(iv) -23/80
(v) – 15/66
In case of terminating decimals, write their decimal expansions.
Q2 Express the following recurring decimals as vulgar fract/JPEGions:
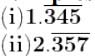
Q3 Insert a rational number between 5/9 and 7/13, and arrange in ascending order.
Q4 Insert four rational numbers between 4/5 and 5/6.
Q5 Prove that the reciprocal of an irrational number is irrational.
Q6 Prove that the following numbers are irrational:
Q7 Prove that √3 is a rational number. Hence show that 5 - √3 is an irrational number.
Q8 Prove that the following numbers are irrational:
(i) 3 + √5
(ii) 15 - 2√7
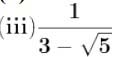
Q9 Rationalise the denominator of the following:
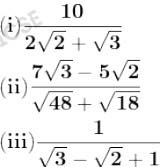
Q10 If p, q are rational numbers and p - √15q = 2√3 - √5/4√3 - 3√5, find the values of p and q.
Q11 If x = 1/3 + 2√2, then find the value of x – 1/x.
Q12 
Q13 Write the following real numbers in descending order:

Q14 Find a rational number and an irrational number between √3 and √5.
Q15 Insert three irrational numbers between 2√3 and 2√5, and arrange in descending order.
Q16 Give an example each of two different irrational numbers, whose
(i) sum is an irrational number.
(ii) product/JPEG is an irrational number.
Q17 Give an example of two different irrational numbers, a and b, where a/b is a rational number.
Q18 If 34.0356 is expressed in the form p/q, where p and q are coprime integers, then what can you say about the fact/JPEGorization of q?
Q19 In each case, state whether the following numbers are rational or irrational. If they are rational and expressed in the form p/q, where p and q are coprime integers, then what can you say about the prime fact/JPEGors of q?
(i) 279.034

(iii) 3.010010001…
(iv) 39.546782
(v) 2.3476817681…
(vi) 59.120120012000…
Contact Us
