Maths Logarithms Exercise9-2
Please Select
Q1 Simplify the following:
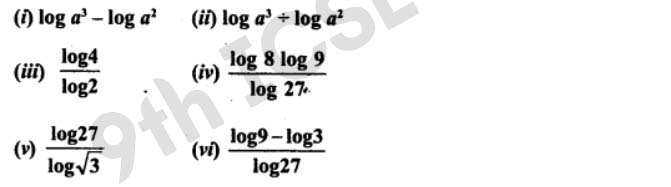
Q2

Q3

Q4 Prove the following :
(i) log10 4 ÷ log10 2 = l0g3 9
(ii) log10 25 + log10 4 = log5 25
Q5
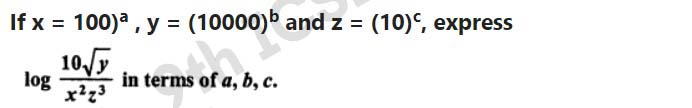
Q6 If a = log10x, find the following in terms of a :
(i) x
(ii) log10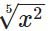
(iii) log105x
Q7
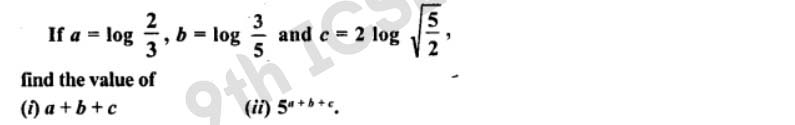
Q8
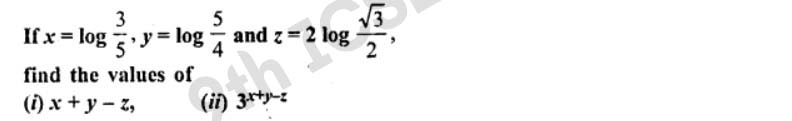
Q9
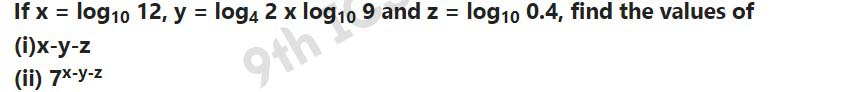
Q10 If log V + log3 = log π + log4 + 3 log r, find V in terns of other quantities.
Q11 Given 3 (log 5 – log3) – (log 5-2 log 6) = 2 – log n , find n.
Q12 Given that log10y + 2 log10x= 2, express y in terms of x.
Q13 Express log102+1 in the from log10x.
Q14
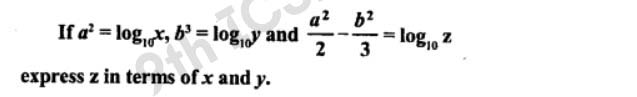
Q15 Given that log m = x + y and log n = x-y, express the value of log m²n in terms of x and y.
Q16
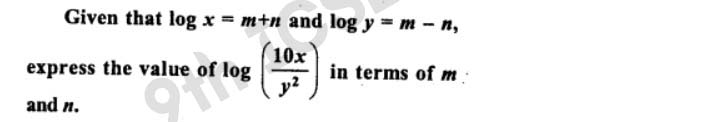
Q17
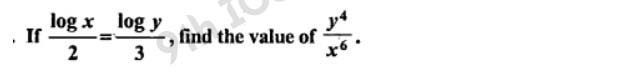
Q18
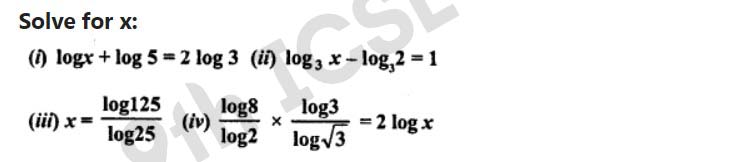
Q19 Given 2 log10x+1= log10250, find
(i) x
(ii) log102x
Q20
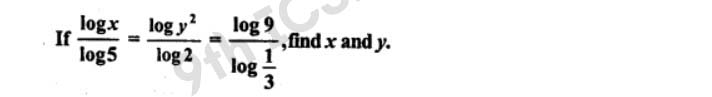
Q21 Prove the following :
(i) 3log 4 = 4log 3
(ii) 27log 2 = 8log 3
Q22 Solve the following equations :
(i) log (2x + 3) = log 7
(ii) log (x +1) + log (x – 1) = log 24
(iii) log (10x + 5) – log (x – 4) = 2
(iv) log105 + log10(5x+1) = log10(x + 5) + 1
(v) log (4y – 3) = log (2y + 1) – log3
(vi) log10(x + 2) + log10(x – 2) = log103 + 31og104.
(vii) log(3x + 2) + log(3x – 2) = 5 log 2.
Q23 Solve for x :
log3 (x + 1) – 1 = 3 + log3 (x – 1)
Q24
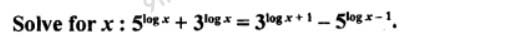
Q25

Q26

Q27 If p = log1020 and q = log1025, find the value of x if 2 log10 (x +1) = 2p – q.
Q28

Q29
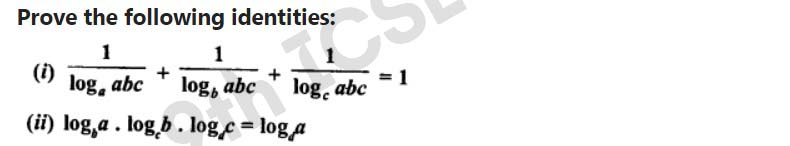
Q30
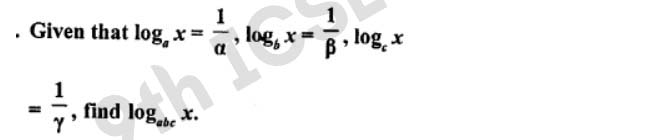
Q31

Contact Us
